Using Talos for Feature Hyperparameter Optimization?

When designing the architecture for an artificial neural network, there exist a variety of parameters that can be tuned. It is indeed an art in itself to find the right combination for these parameters to achieve the highest accuracy and lowest loss. In this blog post, we are testing the usage of Talos for hyperparameter optimization of a neural network.

Just like we have GridSearchCV for hyperparameter optimization within scikit-learn models like Decision Trees / Random Forest and Support Vector Machine, Talos can be applied on Keras models. Talos works similarly to GridSearchCV, by testing all possible combinations of those parameters you have introduced, and chooses the best model, based on what parameter you have asked it to either optimize or reduce.

What is Talos?

Talos was released on May 11, 2018 and has since been upgraded seven times. It works for Python 2 and Python 3, and follows a POD (Prepare, Optimize, Deploy) workflow, to create a flexible and efficient pipeline with state-of-the-art prediction results. When running the code with Talos in the scan-command, all possible combinations are tested in one experiment. The best model is then saved and can be applied just like if you made a neural network using Keras.

Making a Neural Network with Talos

We use the credit card fraud dataset for this experiment.
We drop the features: time and amount, and define X and y, just like we did in previous blog post. We then split our dataset in to train, validate and test, and use SMOTE oversampling strategy for solving the problem with imbalanced dataset.

Now, we start playing with our neural network architecture. We define all parameters that we want our model to test in the following code:

Define parameters

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


from keras.activations import relu, elu

p = {'activation1':[relu, elu],
     'activation2':[relu, elu],
     'optimizer': ['Adam', "RMSprop"],
     'losses': ['logcosh', keras.losses.binary_crossentropy],
     'first_hidden_layer': [10, 8, 6],
     'second_hidden_layer': [2, 4, 6],
     'batch_size': [100, 1000, 10000],
     'epochs': [10, 15]}

We want to test whether relu or elu are the best activation functions for the hidden layers, and test Adam and RMSprop as optimizers. In the original blog post, we used a Tensorflow optimizer. However, Talos do not support this activation function, as it origins from Tensorflow, and not Keras. We also wish to test whether logcosh or binary_crossentropy are the best loss functions. For the architecture, we wish to test if the first hidden layer should have 10, 8 or 6 neurons, and the second hidden layer should have 2, 4, or 6 neurons. If we wanted to test how many hidden layers our neural network architecture should have, we can design another parameter for testing this. However, to be able to run the experiment, we would have to add the test for hidden layers in a parameter dictionary for itself (see Talos).

We additionally test the size of the batches and number of epochs to see which model performs best.

For testing, we design our neural network architecture, almost the same way as when we are designing a neural network by the help of Keras, except we use params for calling our parameters defined above:

Design the neural network architecture

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.activations import sigmoid
from talos import early_stopper

def fraud_model(X_train, y_train, x_val, y_val, params):
    model = Sequential()
    model.add(Dense(params['first_hidden_layer'], 
                    input_shape=(29,), 
                    activation=params['activation1'], 
                    use_bias=True))
    model.add(Dropout(0.2))
    model.add(Dense(params['second_hidden_layer'], 
                    activation=params['activation2'], 
                    use_bias=True))
    model.add(Dropout(0.1))
    model.add(Dense(1, activation=sigmoid))

    model.compile(optimizer=params['optimizer'], 
                  loss=params['losses'], 
                  metrics=[keras.metrics.binary_accuracy])
    history = model.fit(X_train_resampled, 
                    y_train_resampled,
                    batch_size=params['batch_size'],
                    epochs=params['epochs'],
                    verbose=1,
                    validation_data=[X_val_resampled, y_val_resampled],
                    callbacks=[early_stopper(epochs=params['epochs'], 
                                                    mode='moderate', 
                                                    monitor='val_loss')])
    return history, model

By the help of the Scan command, we start configuring the experiment

Use Scan command

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


from talos import Scan

h = Scan(X_train_resampled, 
         y_train_resampled, 
         model=fraud_model, 
         params=p, 
         grid_downsample=0.1,
         print_params=True, 
         dataset_name="creditcardfraud", 
         experiment_no='1', 
         reduction_metric="val_loss", 
         reduce_loss=True)

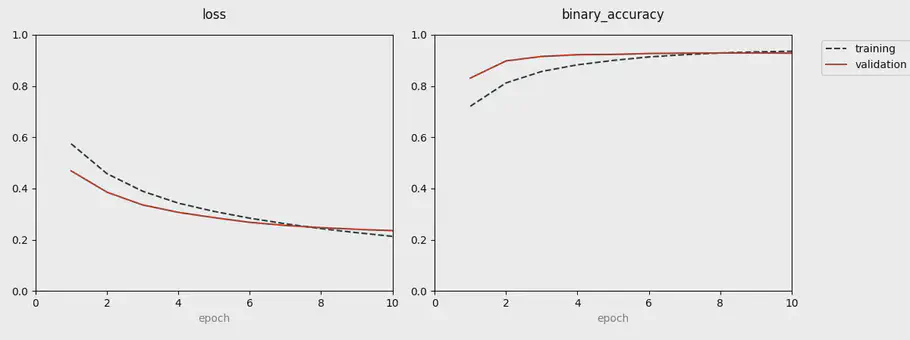
When running the experiment, we can use early stopper or the Live command as callbacks.
Live makes it possible for us to follow the accuracy score and loss of each epoch by the help of a visualization board. It makes it easy to see the performance of each combination. The output looks similar to the picture visualized above.
When we run the scan command, we have a total of 86 experiments, based on all the above combinations.

The next step is to use the Reporting command to evaluate the experiments. Reporting saves a CSV-file where each experiment is stored with its results. In this file, you can see the rounds_epochs, val_loss, val_accuracy, train loss, test accuracy, activation function, and number of neurons for first and second hidden layer, the optimizer and loss function, batch size, and epochs.
By printing the best_params for val_loss, those experiments with the lowest loss value are visualized. In our case, the combination of the below, provides a train_loss of 0.0329 and a train accuracy of 92%. Additionally, we get a validation loss of 0.0337, and a validation accuracy of 91%.:

Neurons in first hidden layer: 10
Neurons in second hidden layer: 2
Activation function first hidden layer: elu
Activation function second hidden layer: elu
Optimizer: Adam
Loss function: Logcosh
Epochs: 15
Batch size: 10000

We are now ready to evaluate the model. We wish to evaluate the model that has the lowest val_loss, defined by the metric parameter.

Evaluate

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


from talos import Evaluate

e = ta.Evaluate(h)
evaluation = e.evaluate(X_test, 
                        y_test, 
                        model_id=None, 
                        folds=folds, 
                        shuffle=True, 
                        metric='val_loss', 
                        asc=True)

If we find the experiment satisfying, we can now Deploy the model.

Deploy

1
2
3


from talos import Deploy

model = Deploy(h, "creditcardfraud_1", metric="val_loss", asc=True)

Deploy command prepares a zip-file that can be transferred to another environment or system. The zip files provides us with information about the experiment in “creditcardfraud_1_results.csv”, the weights of the model, saved as “creditcardfraud_1_model.h5, and the model in a json format: “creditcardfraud_1_model.json”.

After we have used the Deploy command, we can get access to the model and use it for production by the help of the Restore command.

Restore

1
2
3


from talos import Restore

model = Restore('creditcardfraud_1.zip')

Conclusion

Talos is a useful package for solving complex neural network models and decide the right combination of the parameters. The best model can be found by running the code one time, instead of running the code after each change of a single parameter. This does save us time, and makes it easier for us to find the best combinations with the lowest loss values. When making for instance a Long Short-Term Memory (LSTM)-model, there exist a larger amount of parameters to tune, and in this case, it can be useful to use Talos to find the best values, the right amount of neurons, and the number of LSTM-layers. However, we should make sure to keep in mind, that if we are dealing with imbalanced dataset, accuracy scores and loss values are not enough. It might be a good idea to use ROC AUC score as a tuning metric when training, to make sure our model do not discriminate the minor group (in our case the fraudulent transactions). Finally, the Report file provides a significant insight on how well each parameter combination performs and is useful for documentation.

// Maria Hvid, Machine Learning Engineer @ neurospace