If you collect data in your company, you have been faced with the choice of how data should be stored. When we aggregate data, we lose information and this can have consequences especially when we store the data. For example, if we need to use raw data later, it will never be possible for us to recreate it with aggregated data. So we have to start all over again with collecting data. In this blog post, we dive into the consequences of choosing different methods to aggregate data and whether raw data is a better alternative.
In this blog post, we will use the term mean quite a lot. Mean is the statistically word for an average. So when you read the mean, this is the average of a dataset.
If you are in a company that has chosen to aggregate your data, can you explain why this particular method has been chosen? Most companies we meet take the mean of data because it is a good standard. That’s what everyone else does too. But is it a good standard? The answer naturally depends on what kind of data we collect and what purpose the collected data has. There are also other options for aggregating numbers than just taking the mean. And those are the ones we are going to talk about today.
Summary of the 7 tips
We know you’re busy and that’s why we’ve summarized our good advice right here.
- Save raw data if the value of information is greater than the cost of storing the data
- Aggregated data can never become raw data again - however, it is possible to make raw data into aggregated data.
- You lose information by aggregating data - very different data sets can have the same mean.
- Remove outliers before aggregating your data if an anomaly is not important to your value
- Use multiple aggregate methods if you need to aggregate data so that you retain as much information as possible
- More decimals after the comma gives more nuances
- Aggregate data in short intervals - 5 minute intervals gives more nuances than once an hour
In the following sections, we will go more in depth with the consequences of respectively mean and standard deviation, min/max, and quartiles.
Mean and Standard Deviation
Let’s start with the method most often used: the mean. In the picture you can see 4 very different data sets.
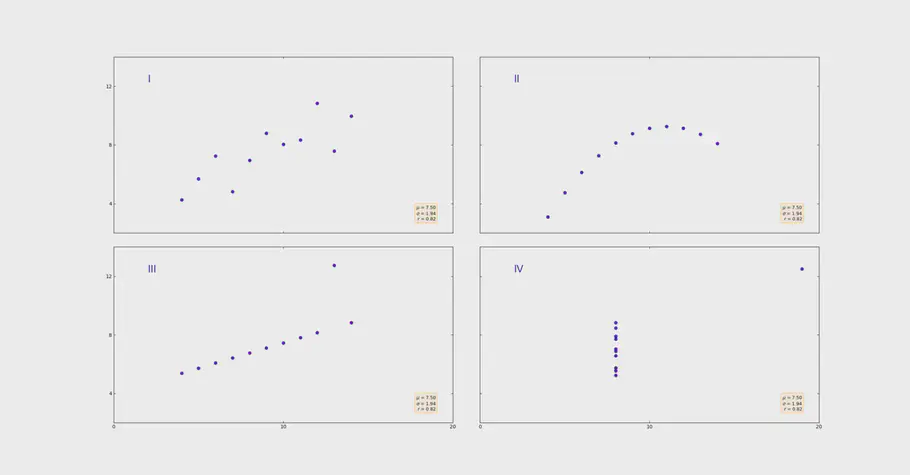
4. different datasets
However, what they have in common is that they have exactly the same mean of 7.50. But as we can see, the mean stores information on how the dataset is distributed. Pictures 1 and 2 show a nice trend, while pictures 3 and 4 show data points that store anomalies. Anomalies significantly distort the mean.
Anscombes Quartet, different datasets with same mean and standard deviation
Therefore, it is always recommended to remove anomalies with outlier detection if aggregating data to an average value. An easy way to remove the most extreme values is by making a trimmed mean. However, removing anomalies can also have consequences. If we e.g. are looking at vibrations, it is precisely the anomalies that we are interested in, as they show early signs that something has changed. If we remove the anomalies, then we also remove information. Another challenge with a value over an hour is that we can not say anything about the development. If we compare this hour with the mean of the last hour, we will be able to see if the mean value is increasing or decreasing. But we can say nothing about whether there have been rising and falling values in the given hour.
A good way to supplement the mean is to take the standard deviation. The problem, however, is that the 4 graphs shown in the example also all have the same standard deviation.
| Dataset | Mean | Standard deviation |
|---|---|---|
| I | 7.50 | 1.94 |
| II | 7.50 | 1.94 |
| III | 7.50 | 1.94 |
| IV | 7.50 | 1.94 |
The standard deviation helps to provide more insight than the mean alone can. But in this case, it is not enough that we save both the mean and standard deviation of our data if we want to be able to see the details.
Minimum og Maximum
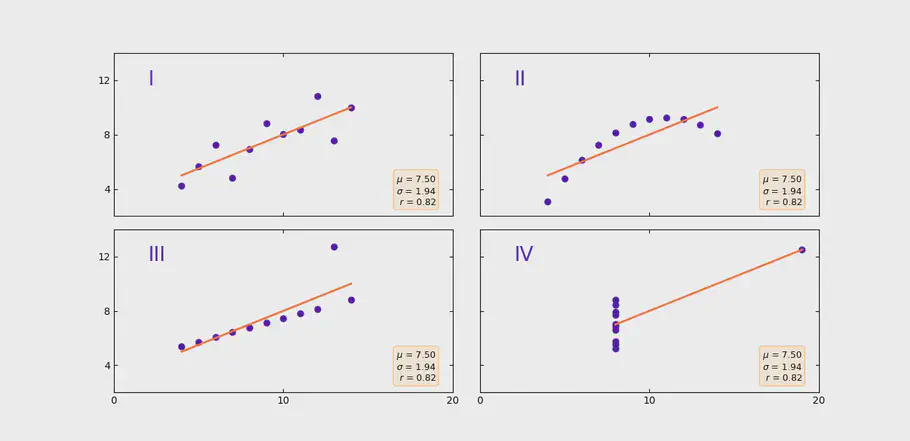
Another recognized way of storing information about data is by storing the smallest and largest observation identified over a given time interval. If a machine has been out of service for a short time, the smallest number you see will always be 0. You will therefore have nothing else to relate to than that we in this hour went from 0 to 100, which is the maximum value. Whether you are still at 100 and how long there has been a measurement of 100, you do not know. Another challenge is anomalies. At Figure 3 we can see a nice linear trend in our data. Except for one value. Instead of seeing a straight line that goes from 5 to 9, and right through our measured points, the line will be affected by the abnormal maximum value of 12.74. By simply saving the minimum and maximum value, we will thus be able to assume that our data increases steadily from 5 to 12 over the given hour. But the reality is that our data is being displaced by an anomaly, as shown in the image below.
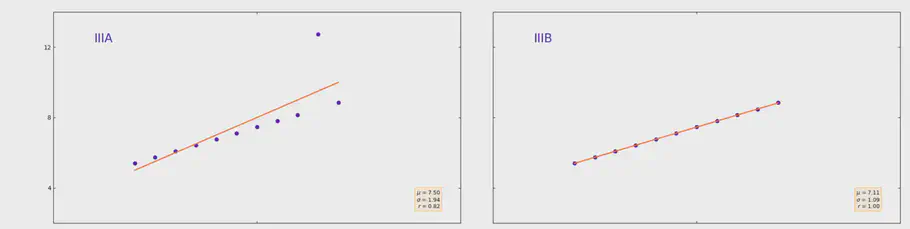
Linear regression with or without anomalies
The four data sets in the example have the same mean and standard deviation, but different minimum and maximum values.
| Dataset | Minimum | Maximum |
|---|---|---|
| I | 4.26 | 10.84 |
| II | 3.10 | 09.26 |
| III | 5.39 | 12.74 |
| IV | 5.25 | 12.50 |
But can we say something from the following numbers, can you tell me something about the trend we see in the picture with the four different data sets? What would you assume if you could just see the minimum and maximum of the datasets?
Quartiles and Median
A good way to get more information about data is by saving quartiles. Quartiles are stored as 0.25, 0.50, 0.75 and 1.00 quartiles, and provide good insight into the distribution of your data set. Quartiles can help us better understand the distribution in our data.
| Dataset | 0.25-quartile | 0.50-quartile (median) | 0.75-quartile | 1.00-quartile |
|---|---|---|---|---|
| I | 6.31 | 7.58 | 8.57 | 10.84 |
| II | 6.70 | 7.14 | 8.95 | 09.26 |
| III | 6.25 | 7.11 | 7.98 | 12.74 |
| IV | 6.17 | 7.04 | 8.19 | 12.50 |
As you can see from the quartiles above, it is much easier to identify the two anomalies in dataset III and dataset IV. When we look at the value from the 0.75 quartile to the 1.00 quartile, it is clear to see that very little data moves relatively quickly compared to the other quartiles. And that's exactly why quartiles are really good parameters if you want to aggregate your numbers over a given period.
Raw data
As far as possible it is always best to save data in raw format. With raw data, we have all the information we need, and depending on what this data is to be used for, it can be aggregated in the way that best suits the given case. Why not just save all data in raw format? One of the reasons is without a doubt the cost of storing large amounts of data. For example, if you collect data from accelerometers and store them in a raw format, you can quickly get up and collect more than 24 mega bytes per asset per day.
But it is important here to keep in mind that hard drive prices have dropped a lot over time and therefore it has also become cheaper and cheaper to store data. Eg. you can save 1 tera byte or the same as 41667 days of data from your asset for DKK 125 per month. So the mindset around that raw data is expensive to save maybe belongs to the past. What you need to consider is whether the value of information is higher than the cost of storing “a lot” of data because it is raw.
Decimals matter
In the example we have used through the blog post, we have had exactly the same mean and standard deviation. If we allowed more than 2 decimal, we would see a small difference in the standard deviation. Therefore, more decimals help to make your dataset more nuanced. The actual standard deviations of the four data sets can be seen in the table.
| Dataset | Standard Deviation (to decimals) | Standard Deviation (more decimals) |
|---|---|---|
| I | 1.94 | 1.9370243 |
| II | 1.94 | 1.9371087 |
| III | 1.94 | 1.9359329 |
| IV | 1.94 | 1.9360806 |
As you can see, nuances appear and we can now see the details of the standard deviation and that they are not exactly the same. Decimals thus allow us to capture all the nuances.
7 tips
How you best store your data depends on what data you are collecting and for what purpose the data is to be used subsequently. If you choose or may have already chosen to store aggregate numbers with one of the aforementioned methods, we will recommend you to use multiple aggregation methods. This could, for example, be to store both the mean and the median for a given period. Saving the 4 quartiles allows you to understand how the data set is distributed, while the minimum and maximum do not say anything about the distribution between the minimum and maximum values. Remember to deal with anomalies if you aggregate your numbers. Anomalies significantly affect both mean and min / max values. If you do not need to use the anomalies for anything, these must be handled before you aggregate your numbers.
Storing data in a raw format can be expensive, but it is also the method that gives you the most information. Every time we aggregate numbers we lose information. It is therefore always recommended to save data in as raw a format as possible. If you are forced to aggregate the numbers, our clear recommendation is that you aggregate your data in small intervals. Instead of saving your data in hourly values, you will get more transparency by saving it as, for example, 5-minute values. This means that instead of having 1 measurement per hour, you have 12 measurements for each hour.
Our clear recommendation is to assess whether you should save raw data: If the value of information is greater than the cost of storing the data, save the data raw. Aggregate numbers are not possible to make into raw data, but it is easy to convert raw data to aggregated numbers. If raw data is not saved, you can never get the raw values back. If you later find out that you need to use your data for something that requires raw data, you are forced to start all over again with the data collection.
The 7 tips for data collection are as follows:
- Save raw data if the value of information is greater than the cost of storing the data
- Aggregated data can never become raw data again - however, it is possible to make raw data into aggregated data.
- You lose information by aggregating data - very different data sets can have the same average.
- Remove outliers before aggregating your data if an anomaly is not important to your value
- Use multiple aggregate methods if you need to aggregate data so that you retain as much information as possible
- More decimals after the comma gives more nuances
- Aggregate data in short intervals - 5 minute intervals gives more nuances than once an hour
// Maria Hvid, Machine Learning Engineer og Rasmus Steiniche, CEO @ neurospace