Hvilken model præstere det bedste resultat med at detektere kvaliteten på rødvin; Kunstig neurale netværk eller Support Vector Machine?

Når du håndterer et problem, skal du bestemme, hvilken model du skal bruge til at løse det. Du kan vælge mellem to tilgange: statistik eller maskinlæring. Hvis statistik ikke kan løse problemet, er det tid til at eksperimentere med maskinlæring og finde ud af, hvilken model der skal bruges. I dag er et øget fokus på brugen af kunstige neurale netværk, som er en stærk arkitektur til løsning af komplekse problemer. Glem dog ikke, at der indenfor maskinlæring findes andre stærke algoritmer, såsom decision trees, random forests, og support vector machines. Følgende tilfælde er et opgør mellem kunstige neurale netværk og support vector machines, når man bestemmer kvaliteten af rødvin.
Dette datasæt er interessant, fordi det kræver, at du gennemgår outlier detektion, korrelationstest, det er et ubalanceret datasæt, med manglende information, og til sidst kan vi registrere, hvor godt to stærke algoritmer fungerer på samme vilkår.
Introduktion til datasættet
Det tilgængelige datasæt er fra Kaggle. Dataene er indsamlet af fem vineksperter P. Cortez, A Cerdeira, F. Almeida, T. Matos og J. Reis. Al vin, der er smagt, er fra den samme provins i Portugal og består af i alt 1599 røde vine og 4898 hvide vine. Hver vin er blevet evalueret gennem en score mellem nul (meget lav) til ti (meget høj) [1].
Datasættet indeholder 11 input features:
- Fast syreindhold
- Flygtig syreindhold
- Citronsyre
- Rest sukker
- Klorid
- Fri svovldioxid
- Samlet svovldioxid
- Massefylde
- pH
- Sulfater
- Alkohol
og en outputvariabel: Kvalitet
På grund af privatlivets fred og logistiske problemer informerer datasættet ikke om typen vindrue, salgspris eller vinmærke. Der gives heller ingen oplysninger om, hvordan de fem forfattere bestemmer score (anonymt, gennemsnit af total score osv.).
Udforsk rødvins datasættet
Datasættet har ingen manglende værdier og er i udforskningsfasen opdelt til rødvin og hvidvin, fordi vi har en hypotese om, at feature vigtighed er forskellig for rødvin og hvidvin. Til dette opgør vil vi kun se på rødvin. For at få en forståelse af fordelingen kan vi se på, hvor mange observationer der præsenteres på hvert kvalitetsniveau (0 - 10):
|
|
| Kvalitet | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| n | 10 | 53 | 681 | 638 | 199 | 18 |
| procent | 0.63% | 3.31% | 42.59% | 39.90% | 12.45% | 1.13% |
Baseret på dette kan det konkluderes, at datasættet er meget ubalanceret. Ikke nok med at størstedelen af rødvine klassificeret er klassificeret med et kvalitetsniveau på 5 eller 6, der findes heller ingen observationer i hver ende af skalaen, hvilket gør det svært for vores model at lære om disse fem scoringer (0 til 2, og 9 til 10).
Korrelation og HeatMap
For at se, om der findes en visuel lineær sammenhæng mellem inputfunktionerne og outputvariablen, kan vi bruge søjlediagrammer. Vi vil bruge seaborn til at oprette disse plots med kun få linjer kode:
|
|
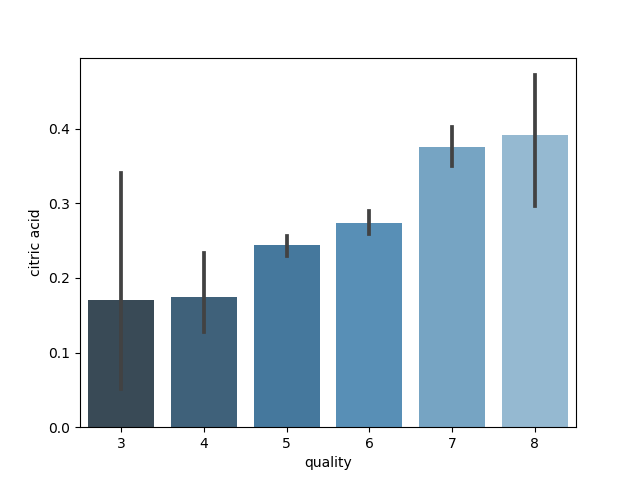
Barplot for citronsyre
Selvom søjlediagrammet indikerer et lineært forhold, er det vanskeligt at være sikker, fordi konfidensniveauet viser en usikkerhed. Derfor foretages en Spearman-korrelationstest for at få en forståelse af sammenhængenes styrke. Først designer vi et heatmap med p-værdien bestemt ved følgende kode:
|
|
Beslutningsreglen er, at hvis p-værdien er under 0,05, afvises nulhypotesen om rho = 0, og korrelationen er signifikant. Gennem denne test bestemmes det, at flygtig syreindhold ikke giver nogen væsentlig indflydelse på modellen, hvorpå denne fjernes. Derimod synes alkohol at være det vigtigste parameter for outputvariablen med en positiv lineær korrelation på 0,48, og densiteten er positivt lineær korreleret med mængden af resterende sukker (0,42), chlorid (0,41), citronsyre (0,35) og fast syreindhold (0,62) Derudover har pH-værdien et negativt lineært forhold til mængden af fast syreindhold (-0,71), citronsyre (-0,55) og chlorid (-0,23). Imidlertid er ingen af inputværdierne stærkt positive eller negativt korrelerede med outputvariablen.
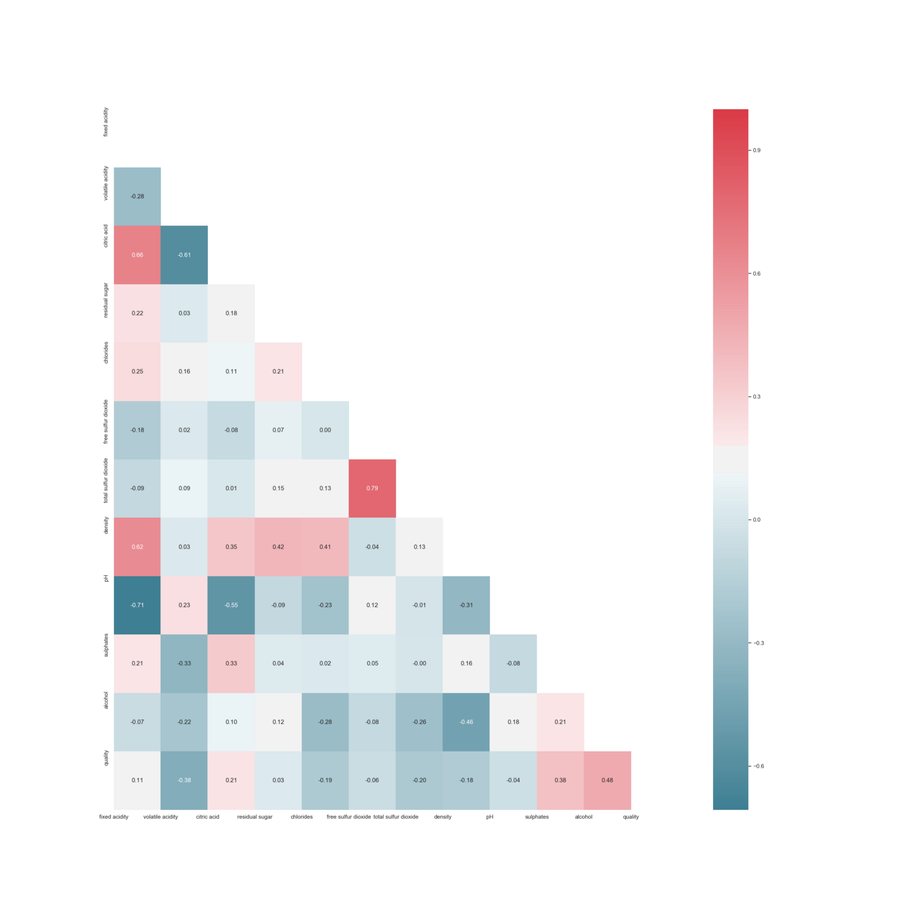
HeatMap med Spearman korrelation
Anomali påvisning
De tidligere bar plots indikere at der findes en høj standardafvigelse i begge ender af output skalaen. Hver gennemsnit og standardafvigelse for inputfunktioner beregnes, hvilket bekræfter dette. Vi kan bruge Swarm plot for at visualisere disse anomalier.
|
|
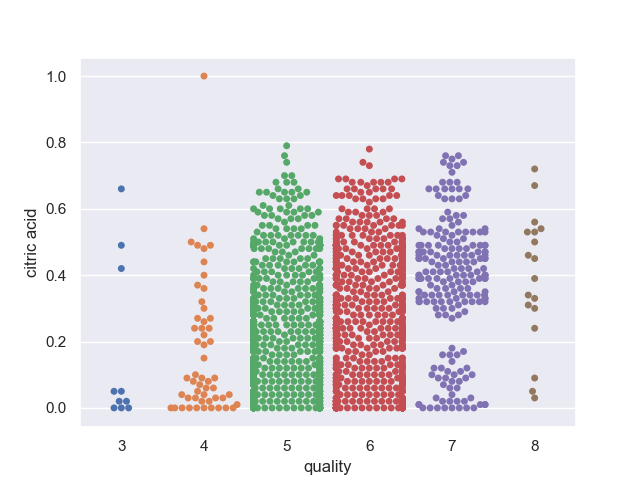
Swarmplot for citronsyre
Generelt i alle swarmplots angiver næsten alle klasser undtagen hvor kvaliteten er 5 og 6, at der er nogle anomalier.
Et problem med kvalitetsniveauet 3 og 8 er den lille mængde repræsentanter, hvilket gør det svært at finde et mønster.
De detekterede anomalier kan enten fjernes manuelt eller ved statistiske test, der automatisk fjerner disse. Vi har brugt Tukey’s test til automatisk at opdage og fjerne anomalier, hvilket resultere i, at vi fjerner 255 observationer, der giver et datasæt på 1.343 observationer.
Dette får vores forbedrede datasæt til at se sådan ud:
| Kvalitets grupper | Repræsentanter |
|---|---|
| 3 | 4 |
| 4 | 41 |
| 5 | 574 |
| 6 | 549 |
| 7 | 161 |
| 8 | 14 |
Ubalanceret datasæt
I henhold til outputvariablen forventes det at være i stand til at forudsige den nøjagtige score for en vin i en skala fra 0 til 10. Imidlertid introducerer vi vores model til et datasæt med kun få repræsentanter i skalaens middelklasse, samt ingen repræsentanter i begge ender af skalaen. Hvad vi kan gøre i stedet er at ændre dette til et binært problem: Hvis den givne score er højere end eller lig med 7, er vinen af høj kvalitet, og værdier under denne tærskel er af lav kvalitet.
For at bruge vores algoritmer er vi nødt til at opdele datasættet i træn og test. Når du ændrer outputvariablen til en binær variabel med 0 hvis lav kvalitet og 1 hvis høj kvalitet, er antallet af repræsentanter for høj og lav kvalitet i trænings datasættet som følger:
| n_0 (lav kvalitet) | 929 |
|---|---|
| n_1 (høj kvalitet) | 145 |
Vi har drøftet ubalanceret datasæt i forrige blogindlæg, og der er desuden brugt SMOTE-oversamplingsstrategi for dette problem også, hvilket har medført at træningsdatasættet nu har en størrelse på = 1.858 observationer. Dette er fantastisk, vores datasæt er klar til at blive brugt sammen med et neuralt netværk og en support vector machine algoritme. Vi vil bruge det nøjagtig samme datasæt til et neuralt netværk og en support vector machine for at se, hvor godt de klarer sig på nøjagtigt samme vilkår.
Neural Netværk
Lad os først se, hvor godt et neuralt netværk kan forudsige kvaliteten af rødvin.
|
|
Vi har konstrueret et simpelt neuralt netværksarkitektur med et skjult lag. Tilføjelse af flere skjulte lag forbedrer ikke trænings - og heller ikke testnøjagtigheden. Et dybt neuralt netværk er derfor ikke nødvendigt for dette problem. Træningsnøjagtigheden er på 83,32% med en testnøjagtighed på 82,90%. Tabet på træn og test adskiller sig ikke væsentligt fra hinanden. Derudover har vi en area under curve-score på 90,79%.
Support Vektor Maskine
Lad os nu se, hvor godt en support vector machine kan forudsige kvaliteten af rødvin Input:
|
|
Ved hjælp af GridSearchCV er vores C-værdi indstillet til at være 2,0, hvilket giver en træningsnøjagtighed på 91,53% og en testnøjagtighed på 90,33%.
Opsummering
Vi har forberedt vores datasæt, detekteret anomalier, fjernet features, der ikke har en signifikant korrelation, og behandlet et ubalanceret datasæt. Vi har testet det nøjagtig samme datasæt med to forskellige algoritmer: et neuralt netværk og en support vector machine. Følgende tabel opsummerer, hvor godt det neurale netværk og support vector machine fungerer på dette rødvins datasæt.
| Neural Netværk | Support Vektor Maskine | |
|---|---|---|
| Trænings nøjagtighed | 83,32% | 91,53% |
| Test nøjagtighed | 82,90% | 90,33% |
Derudover ændres vores tab eller fejlværdi ikke væsentligt fra træn til test. Som en konklusion har vores support vector machine en 8 procentpoint højere nøjagtighed sammenlignet med vores neurale netværksmodel.
Bekymringer omkring datasættet
Datasættet er samlet af fem vineksperter, der kun smager vinen fra en provins, hvilket reducerer generaliserbarheden til andre områder. Det er ukendt, hvor mange år vinene, der er smagt, er blevet opbevaret, samt typen af vintruer. Det er endvidere ukendt, hvordan forfatterne har scoret vinene. Hvis det ikke er gjort annonymt, kan der være introduceret bias i datasættet. Derudover er en score fra 0 til 10 en bred score, hvor en score på 1 til 5 ville være bedre og mere præcis [2].
Som en sidebemærkning til dig næste gang du står i en vinbutik og beslutter, hvilken vin du skal købe, kan en god tommelfingerregel være at gå for en høj alkoholprocent, hvis du ikke kan smage den, før du køber den.
Og vinderen er…
For et problem, der ikke kræver mere end et skjult lag, og som ikke er ekstremt kompliceret, giver en support vector machine det bedste resultat sammenlignet med en kunstig neuralt netværksalgoritme.
Husk altid at løse problemerne med målet om at få den bedst mulige løsning, ikke den mest avancerede arkitektur.
// Maria Hvid, Machine Learning Engineer @ neurospace