“Reducer energiforbruget i din husstand, så lever du længere”.
Dette kan være en overskrift i din foretrukne avis.
Mennesker har en tendens til at se en korrelation mellem to værdier og bestemmer straks, at der er kausalitet. Kausalitet er det samme som årssagssammenhæng og begge udtryk vil blive anvendt i denne blog post
Men ville du virkelig leve længere uden energi i din husstand?
Korrelation er nøglen til enhver god statistisk analyse og til at løse problemer med maskinlæring.
En sammenhæng mellem to værdier som husholdningens energiforbrug og gennemsnitlig levetid, betyder ikke nødvendigvis, at der er en årsagssammenhæng.
Men hvad betyder det, at to værdier er korrelerede, og hvorfor er det vigtigt i maskinlæring? Dette blogindlæg har til formål at give dig en forståelse af, hvad korrelation og årsagssammenhæng er.
Definitioner
Først skal vi forstå, hvad korrelation og årsagssammenhæng betyder. En måde at gøre dette på er igennem definitioner:
en korrelation beskrives som gensidig sammenhæng imellem to eller flere værdier.
en årsagssammenhæng beskriver, når værdier har et forhold mellem årsag og virkning. Eller med andre ord du kan forklare et resultat baseret på et andet.
Korrelation
Groft sagt svarer en sammenhæng på spørgsmålet: “Hvordan kan meget af ændringen i X også ses i Y?”.
Hvis den ene værdi stiger med en faktor 2, indebærer en sammenhæng, at vi derudover kan se en lignende ændring i den anden værdi. Korrelation udtrykkes som en værdi mellem -1 og +1, hvor;
| Korrelation( r ) | Fortolkning |
|---|---|
| -1 | En perfekt (negative) lineær relation |
| -0.7 | En stærk negativ lineær relation |
| -0.5 | En moderat negativ lineær relation |
| -0.3 | En svag negativ lineær relation |
| 0.0 | Ingen lineær relation |
| +0.3 | En svag positiv lineær relation |
| +0.5 | En moderat positiv lineær relation |
| +0.7 | En stærk positiv lineær relation |
| +1.0 | En perfekt positiv) lineær relation |
En korrelation kan være både positiv og negativ hvilket definerer hvordan værdierne hænger sammen. Hvis korrelationen er positiv, indebærer det en gensidig stigning eller fald i både x og y. Hvis korrelationen er negativ, indebærer det en modsat stigning eller fald i x- og y-værdier.
Forbindelsen mellem to variabler kan bruges til at forudsige hinanden. Hvis du har en værdi, kan du sige noget om hvorvidt den anden værdi stiger eller falder. Korrelationer er nøglen til at løse problemer med statistik såvel som maskinlæring, da de bruges til at udtrykke og se, hvilke værdier der er vigtige for det problem, vi prøver at løse (f.eks. Forudsigelse af fremtidige maskinnedbrud).
En korrelation har også et signifikansniveau. Signifikansniveau er en faldgrube, som folk glemmer at kontrollere. Du kan have en stærk sammenhæng mellem to værdier, men ingen betydning. I dette tilfælde er der ingen bevis for, at den korrelation vi har identificeret, er sand.
Tilbage til hvor vi begyndte ”_ Reducer energiforbruget i din husstand, og du vil leve længere_” ifølge tal fra Danmarks Statistik. Men er dette virkelig sandt?
Hvis vi ser efter er der en stærk negativ korrelation (r = -0,83) mellem gennemsnitlig levetid og husholdningens energiforbrug baseret på data tilgængelige fra Danmarks Statistik fra 2008 - 2017. Korrelationen er yderligere signifikant 0,00317, hvor værdien gerne skal være så lav som muligt.
Gennemsnitlig levealder (i år)
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|---|
| 78.5 | 78.7 | 79.2 | 79.5 | 79.9 | 80.0 | 80.6 | 80.1 | 80.4 | 80.6 |
Energi forbruget i husholdninger, total (i GJ)
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|---|
| 346030085 | 344461450 | 359692114 | 331398746 | 325059155 | 328585821 | 308098658 | 312899498 | 326690453 | 318506670 |
I henhold til vores indledende analyse er de to variabler, gennemsnitlig levetid og energiforbrug i husholdninger, stærkt negativt korrelerede. Der er dog nogle almindelige faldgruber vi skal overveje før vi konkluderer, at der er kausalitet. Derudover er vi nødt til at validere om vi kan stole på resultatet.
1) Datasættets størrelse
Baseret på hvad der er tilgængeligt fra Danmarks Statistik, har vi et lille datasæt bestående af kun 9 observationer. Korrelationen vi ser her, selvom den er betydelig, kan være en tilfældighed fordi vi ikke har et stort nok datasæt.
2) Er de forbundet i den virkelige verden?
Hvordan kan det være rigtigt, at energiforbruget i husholdninger er korreleret med vores gennemsnitlige levetid? Det er sandsynligvis ikke korrekt. Korrelationer siger, hvordan værdier er gensidigt forbundet baseret på tendensen - hvis den ene værdi stiger, stiger eller falder den anden værdi?
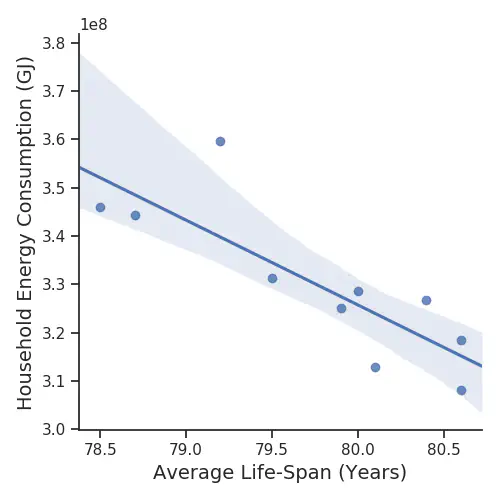
Så hvad vi har brug for, er sammenhænge der er forbundet med det problem vi ønsker at løse. Hvad påvirker i dette tilfælde vores gennemsnitlige levetid? Som det kan ses på grafen, er der en afvigelse i den tredje værdi. Hvis der er en stærk sammenhæng, skal denne afvigelse i energiforbruget også ses i den gennemsnitlige levetid. Det er der ikke, det indikerer at energiforbruget i husholdningen muligvis ikke er den bedste måde at forudsige den gennemsnitlige levetid på.
Kausalitet
Mange mener at korrelation er lig med årsagssammenhæng og dermed titlen på dette blogindlæg. Det er dog ikke nødvendigvis sandheden. Årsagssammenhæng findes kun hvis vi kan sige noget om årsag og virkning: ”Hvor meget af ændringen i X kan forklares med Y?”. I vores tilfælde: Hvor meget kan ændringen i husholdningens energiforbrug (årsag) forklare den gennemsnitlige levetid (virkning)?
Årsagen er vanskelig at måle og kan kun baseres på store datasæt og grundig analyse. En måde er at bruge en additiv støjmodel.
Årsagen sigter mod at identificere årsag og virkning - forholdet. Én fremgangsmåde til at gøre dette er ved at se på om der også kan ses unormale observationer i en variabel.
Vi ser en høj stigning i husholdningens energiforbrug i 2010, hvoraf værdien af den gennemsnitlige levetid yderligere øges lidt. Ifølge vores korrelationsanalyse skulle den gennemsnitlige levetid imidlertid være faldet markant i dette år som en årsag til et øget energiforbrug i husholdningen.
Så lever du virkelig længere ved at reducere dit energiforbrug i din husstand? Nej Der er en sammenhæng mellem de to variabler, men der er ingen årsagssammenhæng. Du kan ikke bruge energiforbruget i hver eneste husstand i dit nabolag og beregne den gennemsnitlige levetid i dit område. Derudover er det indsamlede datasæt for lille. Hvis vi havde et større datasæt ser vi måske, at denne korrelation bliver ubetydelig.
Hvordan anvender vi korrelationer og kausalitet i maskinlæring
For at kunne forudsige et givet resultat har vi brug for inputdata, der kan forklare det ønskede resultat.
Hvis vi laver en prognosemodel til at forudsige efterspørgsel efter is, betragtes vejret som en vigtig parameter: når det er varmt ønsker vi mere is og kolde ting.
Når vi forudsiger salget af juletræer, vil sæsonen være en vigtig faktor: fordi vi bruger flere juletræer i løbet af december end resten af året.
Prædiktiv vedligeholdelse på roterende udstyr kan bruges til at forudsige nedbrud i den nærmeste fremtid. For at kunne gøre dette skal de relevante data skaffes, som kan sige noget om hvordan udstyret fungerer. Vi ved at vibrationer, temperatur og lyd kan indikere dette.
Når maskinen begynder at vibrere mere end normalt, kan der være noget galt. Hvorfor? Fordi det ikke er normal driftsadfærd, hvilket gør vibrationer til en vigtig måling til at forudsige vores målresultat.
Det samme gælder temperatur. Hvis maskinen overophedes ved vi at der er noget galt, og så videre.
Konklusion
Stol ikke altid på en korrelation. En korrelation angiver blot om der er en gensidig opadgående eller nedadgående forbindelse mellem to værdier. En sammenhæng skal være væsentlig før det er muligt at sige noget om sammenhæng og årsag. Korrelation betyder ikke, at den ene værdi direkte har indflydelse på den anden - det er derfor, du er nødt til at tjekke for årsagssammenhæng! Antag ikke automatisk at korrelation er årsagssammenhæng.
// Maria Hvid, Machine Learning Engineer @ neurospace