Hvis du opsamler data i din virksomhed, har du stået overfor valget omkring hvordan data skal gemmes. Når vi aggregere data, mister vi information, og det kan have konsekvenser særligt når vi gemmer dataen. Hvis vi eksempelvis skal bruge data i rå format senere, vil det aldrig være muligt for os, at genskabe denne, med aggregerede data. Vi skal altså starte forfra med at opsamle data. I denne blog post dykker vi ned i hvilke konsekvenser det har, når vi vælger forskellige metoder til at aggregere data og om rådata er et bedre alternativ.
Hvis du sidder i en virksomhed som har valgt at aggregere jeres data, kan du forklare hvorfor netop denne metode er valgt? De fleste virksomheder vi møder, tager gennemsnittet af data, fordi det er en god standard. Det er hvad alle de andre også gør. Men er det nu også en god standard? Svaret afhænger naturligt af hvad det er for noget data vi opsamler, og hvilket formål det opsamlede data har. Der findes også andre muligheder for at aggregere tal end blot at tage et gennemsnit. Og det er dem vi skal snakke om i dag.
Opsummering af de 7 råd
Vi ved du har travlt og derfor har vi opsummeret vores gode råd lige her.
- Gem rådata hvis værdien af information er større end omkostningerne ved at opbevare dataen
- Aggregeret data kan aldrig blive til rådata igen - det er dog muligt at lave rådata til aggregerede data.
- Du mister information ved at aggregere data - meget forskellige datasæt kan have samme gennemsnit.
- Fjern outliers inden du aggregere dit data hvis anomalier ikke er vigtige for din værdi
- Brug multiple aggregerings metoder, hvis du skal aggregere data så du bibeholder så meget information som muligt
- Flere decimaler efter kommaet giver flere nuancer
- Aggreger data i korte intervaller - 5 minutters intervaller giver flere nuancer end en gang i timen
I de efterfølgende afsnit vil vi gå mere i dybden med konsekvenserne med hhv. gennemsnit og standardafvigelse, min / max, og kvartiler.
Gennemsnit og Standardafvigelse
Lad os starte med den metode, som oftest bliver brugt: gennemsnittet. På billedet kan du se 4 meget forskellige datasæts.
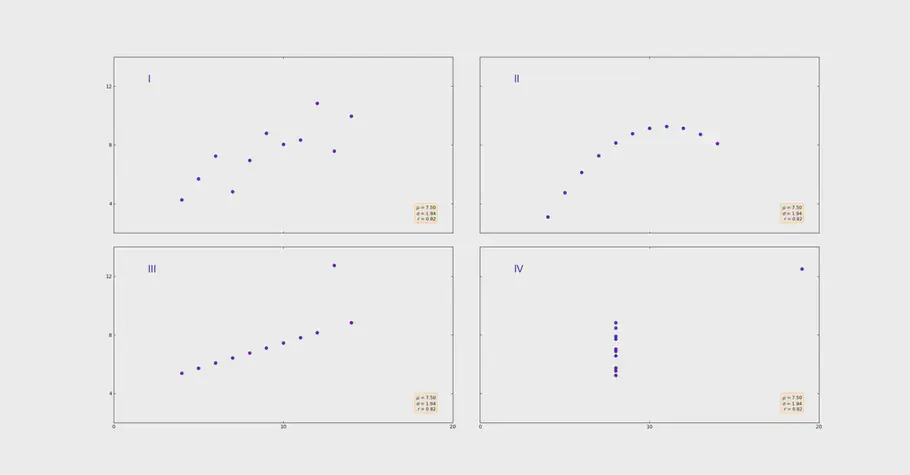
4. forskellige datasæt
De har dog det tilfælles, at de har præcis samme gennemsnit på 7,50. Men som vi kan se, gemmer gennemsnittet på information om hvordan datasættet er fordelt. Billede 1 og 2 viser en pæn trend, mens billede 3 og 4 viser datapunkter som gemmer anomalier. Anomalier forvrænger gennemsnittet signifikant.
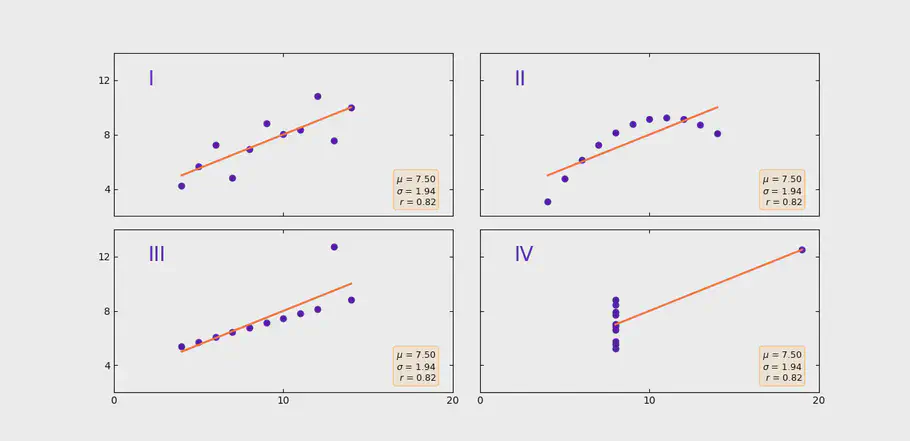
Anscombes Quartet, forskellig datasæt med samme gennemsnit og standardafvigelse
Derfor anbefales det altid at fjerne anomalier, hvis man aggregere data til en gennemsnitlig værdi. En nem måde at fjerne de mest ekstreme værdier, er ved at lave et trimmet gennemsnit. Men at fjerne anomalier kan også have konsekvenser. Hvis vi f.eks. kigger på vibrationer, er det netop anomalierne som vi er interesserede i, da de viser tidelige tegn på at noget har ændret sig. Fjerner vi anomalierne, fjerner vi altså også information. En anden udfordring med en værdi over en time, er at vi ikke kan sige noget om udviklingen. Hvis vi sammenligner denne time med sidste times gennemsnit, vil vi kunne se om den gennemsnitlige værdi er stigende eller faldende. Men vi kan ikke sige noget om, hvorvidt der har været stigende og faldende værdier i den givne time.
En god måde at supplere gennemsnit med, er at tage standardafvigelsen. Problemet er dog, at de 4 grafer vist i eksempelet, også alle har den samme standardafvigelse.
| Datasæt | Gennemsnit | Standardafvigelse |
|---|---|---|
| I | 7,50 | 1,94 |
| II | 7,50 | 1,94 |
| III | 7,50 | 1,94 |
| IV | 7,50 | 1,94 |
Standardafvigelsen er med til at give mere indsigt end hvad gennemsnittet alene kan. Men i dette tilfælde er det altså ikke nok at vi både gemmer gennemsnit og standardafvigelse af vores data hvis vi vil kunne se detaljerne.
Minimum og Maksimum
En anden anderkendt måde at gemme information om data på, er ved at gemme den mindste og største observation identificeret over et givent tidsinterval. Hvis en maskine har været ude af drift i kort tid, vil det mindste tal du ser, altid være 0. Du vil derfor ikke have andet at forholde dig til, end at vi i denne time gik fra 0 til 100, som er den maksimale værdi. Om du stadig er ved 100, og hvor længe der har været en måling på 100, det ved du ikke. En anden udfordring er anomalier. Ved 3. billede kan vi se en pæn lineær trend i vores data. Dog foruden en værdi. I stedet for at se en lige streg som går fra 5 til 9, og lige igennem vores målte punkter, vil stregen være påvirket af den unormale maksværdi på 12,74. Ved blot at gemme minimum og maksimum værdien, vil vi altså kunne antage at vores data stiger støbt fra 5 til 12 henover den givne time. Men virkeligheden er, at vores data bliver forskudt af en anomali, som vist på billedet nedenfor.
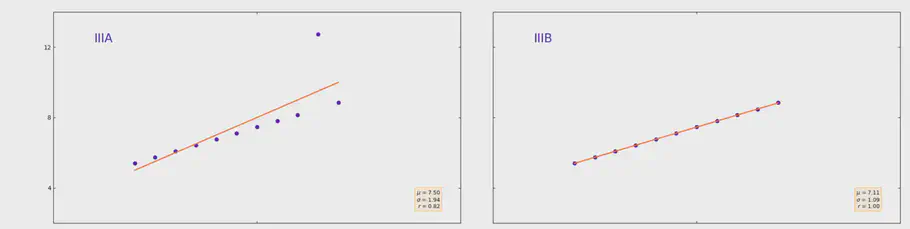
Lineær trend med eller uden anomali
De fire datasæt i eksemplet har samme gennemsnit og standardafvigelse, men forskellige minimum og maksimum værdier.
| Datasæt | Minimum | Maksimum |
|---|---|---|
| I | 4,26 | 10,84 |
| II | 3,10 | 09,26 |
| III | 5,39 | 12,74 |
| IV | 5,25 | 12,50 |
Men kan vi sige noget ud fra følgende tal, kan du fortælle noget om trenden vi ser på billedet med de fire forskellige datasæts? Hvad ville du antage hvis du blot kunne se min og max af datasættene?
Kvartiler og Median
En god måde at få mere information om data på, er ved at gemme kvartiler. Kvartiler gemmes som 0,25, 0,50, 0,75 og 1,00 kvartiler, og giver god indsigt i dit datasæts fordeling. Kvartiler kan hjælpe os til bedre at forstå fordelingen i vores data.
| Datasæt | 0,25-kvartil | 0,50-kvartil (median) | 0,75-kvartil | 1,00-kvartil |
|---|---|---|---|---|
| I | 6,31 | 7,58 | 8,57 | 10,84 |
| II | 6,70 | 7,14 | 8,95 | 09,26 |
| III | 6,25 | 7,11 | 7,98 | 12,74 |
| IV | 6,17 | 7,04 | 8,19 | 12,50 |
Som du kan se ved kvartilerne ovenfor, er det meget nemmere at identificere de to anomalier i datasæt III og datasæt IV. Når vi kigger på værdien fra 0,75-kvartilen til 1,00-kvartilen, er det tydeligt at se at meget lidt data, flytter sig relativ hurtigt sammenlignet med de andre kvartiler. Og lige præcis derfor, er kvartiler rigtig gode parametre, hvis du ønsker at aggregere dine tal over en given periode.
Rådata
Så vidt muligt er det altid bedst at gemme data i rå format. Med rå data har vi al den information vi skal bruge, og alt efter hvad denne data skal bruges til, kan den aggregeres på den måde, som passer bedst til den givne case. Hvorfor gemmer man så ikke bare alt data i rå format? En af årsagerne er uden tvivl omkostningerne ved at gemme store mængder data. Hvis du eksempelvis samler data op fra accelerometere og gemmer dem i rådata, kan du hurtigt komme op og samle mere end 24 megabytes pr asset pr dag.
Men det er vigtigt her at holde i mente at harddisk priserne er faldet meget over tid og derfor er det også blevet billigere og billigere at gemme data. F.eks. kan du gemme 1 terabyte eller det samme som 41667 dage af data fra dit asset for 125 kroner om måneden. Så tankesættet omkring at rådata er dyrt at gemme høre måske fortiden til. Det du skal overveje er om værdien af information er højere end omkostningen ved at gemme “meget” data fordi det er råt.
Decimaler har også en betydning
I eksemplet vi har brugt igennem blog posten, har vi haft præcis samme gennemsnit og standardafvigelse. Hvis vi tillod mere end 2 decimaler efter kommaet, ville vi se en lille forskel i standardafvigelsen. Derfor er flere decimaler med til at gøre dit datasæt mere nuanceret. De faktiske standardafvigelser på de fire datasæt kan du se i tabellen.
| Datasæt | Standardafvigelse (to decimaler) | Standardafvigelse (med flere decimaler) |
|---|---|---|
| I | 1,94 | 1,9370243 |
| II | 1,94 | 1,9371087 |
| III | 1,94 | 1,9359329 |
| IV | 1,94 | 1,9360806 |
Som du kan se dukker der nuancer op og vi kan nu se detaljerne i standardafvigelsen og at de altså ikke er helt ens. Decimaler giver os altså mulighed for at fange alle nuancerne.
7 Gode Råd
Hvordan du bedst gemmer dit data afhænger af dataene du samler op, og til hvilket formål data skal bruges efterfølgende. Hvis du vælger eller måske allerede har valgt at gemme aggregere tal med en af de før-nævnte metoder, vil vi anbefale dig, at benytte multiple aggregerings metoder. Dette kunne eksempelvis være at opbevare både gennemsnit og median for en given periode. Hvis du gemmer de 4 kvartiler giver det mulighed at forstå hvordan datasættet er fordelt, mens minimum og maksimum ikke siger noget om fordelingen imellem minimum og maksimum værdierne. Husk at håndtere anomalier, hvis du aggregere dine tal. Anomalier påvirker både gennemsnit og min / max værdier signifikant. Hvis du ikke skal bruge anomalierne til noget, skal disse håndteres inden du aggregere dine tal.
At gemme data i rådata, kan være dyrt, men er også den metode som giver dig mest information. Hver gang vi aggregere tal mister vi information. Det er derfor altid anbefalet at gemme data i så rå et format som muligt. Hvis du er nødsaget til at aggregere tallene, er vores klare anbefaling at du aggregere dit data i små intervaller. I stedet for at gemme din data i time-værdier, vil du få mere transparens ved at gemme det som eksempelvis 5-minutters værdier. Det vil sige at du i stedet for at have 1 måling pr time, har 12 målinger for hver time.
Vores anbefaling er at vurdere om du skal gemme rådata: Hvis værdien af information er større end omkostningerne ved at opbevare dataen skal du gemme dataen råt. Aggregeret tal er ikke mulige at lave til rådata, men det er nemt at konvertere rådata til aggregeret tal. Gemmes rådata ikke, kan man aldrig få de rå værdier tilbage. Finder du senere ud af at du skal bruge din data til noget som kræver rådata, er du nødsaget til at starte forfra med data-opsamlingen.
De 7 gode råd for data opsamling er som følger:
- Gem rådata hvis værdien af information er større end omkostningerne ved at opbevare dataen
- Aggregeret data kan aldrig blive til rådata igen - det er dog muligt at lave rådata til aggregerede data.
- Du mister information ved at aggregere data - meget forskellige datasæt kan have samme gennemsnit.
- Fjern outliers inden du aggregere dit data hvis anomalier ikke er vigtige for din værdi
- Brug multiple aggregerings metoder, hvis du skal aggregere data så du bibeholder så meget information som muligt
- Flere decimaler efter kommaet giver flere nuancer
- Aggreger data i korte intervaller - 5 minutters intervaller giver flere nuancer end en gang i timen
// Maria Hvid, Machine Learning Engineer og Rasmus Steiniche, CEO @ neurospace